Op deze pagina staan zaken die mij anderszins interesseren. Het heeft meestal te maken met de exacte wetenschappen. Helemaal achteraan staat nog hoe men kerstmis vierde op Rolduc in de negentiende eeuw, in de crypte.
De hoofdstelling van de Galois-theorie door mij opnieuw bewezen.
Wellicht heb je ooit gehoord van Galois-theorie. Welnu dat is een zeer mooie wiskundige theorie die op alle universiteiten met een faculteit wiskunde gegeven wordt en waarover op internet of youtube zeer veel te vinden is. In die theorie is een stelling erg belangrijk en fundamenteel: de hoofdstelling van de Galoistheorie. Meestal wordt die bewezen op de manier zoals Emil Artin [1898-1962] dat gedaan heeft met behulp van een lemma van Dedekind [1831-1916]; maar nog niet zo lang geleden heb ik een ander bewijs voor deze hoofdstelling gevonden door gebruik te maken van de hoofdstelling van de symmetrische polynomen. Ik heb e.e.a in een filmpje gezet en laat Richard Dedekind aan het woord.
Het probleem van de zeven bruggen van Konigsberg.
In dit filmpje wordt het uitgelegd door Leonhard Euler en zijn zoon Johann.
Carl Friedrich Gauss 1777 - 1855
Een aantal filmpjes over hem. Een belangrijk boek dat hij geschreven heeft is -Disquisitiones Mathematicae-. Het is o.a. te verkrijgen in het Engels en Duits. Op internet vind je ook de oorspronkelijke Latijnse versie. Je kunt het ook hier downloaden.
Over Gauss | Over Gauss en Sophie Germain |
Hoe Gauss de som der eerste 100 getallen berekende. | |
Manjul Bhargava
Manjul Bhargava is een zeer getalenteerd wiskundige. Hij heeft zich onder andere bezig gehouden met de Biquadratische vormen, een onderwerp waarmee Gauss in zijn disquisitiones arithmeticae begon. Dirichlet heeft het onderwerp toegankelijker gemaakt.
Platonische lichamen.
Een regelmatig veelvlak of platonisch lichaam is een veelvlak waarvan de zijvlakken regelmatige veelhoeken zijn. Regelmatige veelvlakken zijn convex, hun zijvlakken zijn congruent en alle hoeken tussen de vlakken zijn onderling gelijk. Er bestaan vijf regelmatige veelvlakken.
Émilie du Châtelet 1706-1749.
Emilie is om een aantal zaken interessant. Zij heeft de Principia Mathematica van Newton vertaald in het Frans. Haar vertaling wordt nog steeds gebruikt. Zij heeft ook een eigen filosofie ontwikkeld die in feite een reflectie op allerlei zaken is samenhangend met o.a. het werk van Newton, het werk draagt de titel Institutions de Physique. Bijzonder behalve het milieu van de hoge adel waaruit ze stamt is haar kennissenkring en de geleerden die we bij haar tegenkomen, kortom haar hele netwerk : Voltaire [haar minnaar], Maupertuis, 's Gravesande, Leibniz, Newton, Wolff, Kant, Euler,...Over Emilie zijn best veel boeken geschreven die u makkelijk op internet kunt vinden; meestal zijn het vrouwen die over haar schrijven. Wij volstaan voorlopig met enige youtube filmpjes waar o.a. personen aan bod komen die over haar geschreven hebben. Een website waar veel interessants over haar werken is te vinden is deze . Vooral de pagina over The foundations of physical science van Katherine Brading verdient de aandacht. Zij heeft met een aantal studenten in een seminar de Institutions de Physique vertaald en besproken. Ook is dit in boekvorm uitgegeven bij Routledge.
Een mooi beeld van de omgeving waarin ze leeft en waarmee ze zich bezig houdt.
Fibonacci en Lucas rijen.
De rij van Fibonacci is 1,1,2,3,5,8,13.....en de rij van Lucas is 2,1,3,4,7,11,18.....De rij van quotiënten convergeert naar de Gulden Snede. Mijn bewijs dat ook geldt voor gegeneraliseerde Fibonacci rijen , kun je in de bijgevoegde pdf lezen. Tevens vind je er expliciete formules voor de gegeneraliseerde Fibonacci rijen (genoemd naar Francois Edouard Binet), anders dan de recursie formules. Met behulp van die expliciete formules kun je overigens ook bewijzen dat de rij van de quotiënten naar de Gulden Snede convergeert. Maar kijk eerst de filmpjes op Numberphile over die twee rijen.
Hier rechts is een hele mooie; een mooie eenvoudige afleiding voor een expliciete uitdrukking van Fibonacci en Lucas getallen. | ||
Oliver Byrne, zijn boek uit 1847 over de Elementen van Euclides.
Er is een bijzonder boek over de eerste zes hoofdstukken uit de Elementen van Euclides; het is gedrukt in 1847 en van de hand van Oliver Byrne. Hierbij een aantal filmpjes en websites.
Hier enige websites waar het boek van Oliver Byrne centraal staat
Een schitterende website waar het hele boek van Byrne op staat en meer. | |
Een Nederlands talige site van Jeanne Kok met het hele boek van Byrne. | |
Over het boek van Byrne | |
het boek van Oliver Byrne in pdf |
Filmpjes over het boek De Elementen van Euclides
Hier gaat Wildberger in op het begrip Ratio en de oplossing van Eudoxus om ratio's in zijn algemeenheid te vergelijken. | ||
Eudoxus over Ratio's | Graham Flegg gaat in op de historie van de Elementen van Euclides. Een mooie inleiding. | Hij gaat in op allerlei vroege edities van de Elementen en ook op het werk van Oliver Byrne. Let ook op het driedelige standaardwerk van Thomas Heath. |
Hier een aantal video's van Sandy Bultena die het boek van Euclides redelijk volgt; belangrijk is te zien de gelijkheidsdefinitie van Eudoxus die Sandy aanhaalt in proposition 7 voor ratio's en dan kijken hoe ze daarmee overige zaken bewijst. | ||
Filmpjes van Numberphile; er zijn er veel meer op youtube. Een selectie.
Schleiermacher een interessant persoon.
Friedrich Frobel en Maria Montessori
Een aantal filmpjes over deze twee geweldige pedagogen.
=============================================================
Kerstviering op Rolduc.
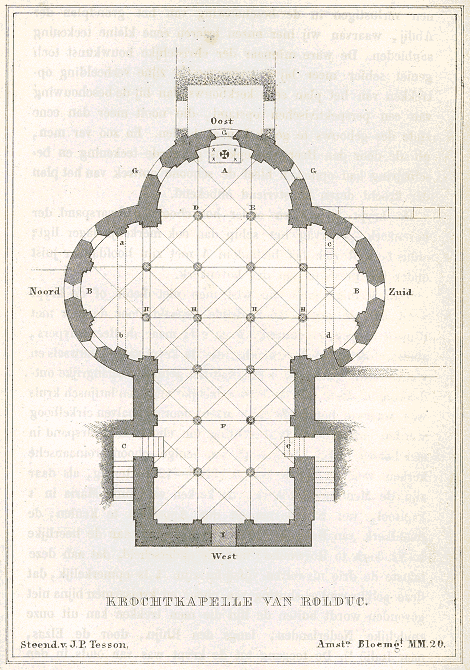
Aan de kerstvieringen die gehouden werden tot aan de eerste wereldoorlog, bestaan mooie herinneringen (zie RJB 1954 pag 82). Het kenmerkende was dat deze kerstvieringen plaatsvonden in de crypte. Als we aannemen dat er zo'n 400 leerlingen waren dan moet dat een hele drukte zijn geweest. De crypte is herhaaldelijk verbouwd en gerestaureerd. De ingang aan de westkant die er nu is tussen de twee trappen naar het koor is er niet altijd geweest, die is er sinds 1873. De sarcofaag van Ailbertus is pas geplaatst in 1897. Voor verdere details zie het gedenkboek 1843-1943 [blz 102/103], Rolduc in Woord en Beeld of het RJB 1927. Hierna het oorspronkelijke plan voor de crypte van Cuypers zoals vermeld in de Dietsche Warande van 1855 en een feitelijke schets van Schaepkens rond 1851. Op het grondplan was a-b en c-d een muur; men kan die muren op de tekening van Schaepkens niet zien; de crypte was dus ooit smaller dan nu. We verzamelen hierna enkele herinneringen van de kerstviering.
De kerstviering geschetst door Emile Coenders; hij zat op Rolduc van 1864-1868. Zie bij diversen het hele boekje van Coenders. De schets van Schaepkens van de crypte komt overeen met de crypte in de tijd van Emile. | |
De kerstviering geschetst door Felix Rutten; hij zat op Rolduc van 1900-1903. Uit het boek Rolduc Schetsen en Herinneringen. De crypte in de tijd van Felix komt overeen met zoals de crypte nu uitziet; uiteraard waren de schilderingen niet gerestaureerd. De sarcofaag en de trap naar het westen was er al. | |
Over de crypte uit RJB 1923; uit RWB en de Dietsche Waranda 1855. | |
Het kerkelijk leven te Rolduc door van Rooy. Ook in de twintigste eeuw waren nog veel van deze gebruiken aan de orde. Adriaan van Rooy was op Rolduc van 1894-1898. | |
Een herinnering van iemand die zowel de toestand meegemaakt heeft van een viering in de crypte en de toestand dat dit niet meer gebeurde; Ook herinnert hij zich hoe Corten zijn rol vervulde bij de kerstviering in de crypte. | |
Lodewijk van Deyssel heeft kerstmis in zijn boek -de kleine republiek- ook beschreven. Zie hier een artikel over dat boek. U treft de beschrijving van kerstmis op blz 52 aan. Lodewijk was op Rolduc van 1875-1878. De crypte komt nog steeds overeen met de schets van Schaepkens, alleen is er extra de trap tussen de twee trappen naar het koor. | |
Venez divin Messie zoals bij Felix Rutten | |
nogmaals | |
Gloria in excelcis Deo zoals bij Emile Coenders | |
Adeste Fideles zoals bij Felix Rutten | |
Rolduc rond 1920 in RJB 1965 , een keerpunt. | |
Elk jaar is er in december een mooi kerstgebeuren op Rolduc , zei de website hiernaast. |
Hierna het -Venez divin Messie- uit het Rolducse zangboek uit 1856 gemaakt door Pothast en versierd door Gerard Slits.